神经网络解决偏微分方程的原理在于通过模拟人脑神经系统的结构和功能，利用大量神经元和连接权重来逼近微分方程的解。通过构建适当的神经网络结构，可以将其训练成能够映射输入与输出关系的近似解算器。这种方法在求解复杂偏微分方程时具有显著优势，特别是在求解高维度、非线性问题以及复杂边界条件的情况下表现突出。神经网络在求解偏微分方程方面的应用广泛，包括物理、工程、金融等领域，为实际问题提供了高效且灵活的解决方案。

本文目录导读：

1. 神经网络的原理
2. 神经网络解偏微分方程的原理
3. 神经网络解偏微分方程的优势
4. 神经网络解偏微分方程的应用
5. 展望

偏微分方程是数学中的一个重要分支，广泛应用于物理、工程、计算机科学等领域，解决偏微分方程通常需要复杂的数学技巧和计算资源，近年来，随着人工智能的飞速发展，神经网络作为一种强大的机器学习工具，被引入到解决偏微分方程的问题中，本文旨在探讨为什么神经网络可以解偏微分方程，以及其背后的原理。

神经网络的原理

神经网络是一种模拟人脑神经元结构的计算模型，通过学习和训练，可以处理复杂的数据并产生预测结果，神经网络的基本单元是神经元，它通过权重连接输入数据，并通过激活函数产生输出，神经网络的训练过程是通过调整权重，使得网络的输出尽可能接近真实结果，这种强大的学习和优化能力使得神经网络在处理复杂问题时具有优势。

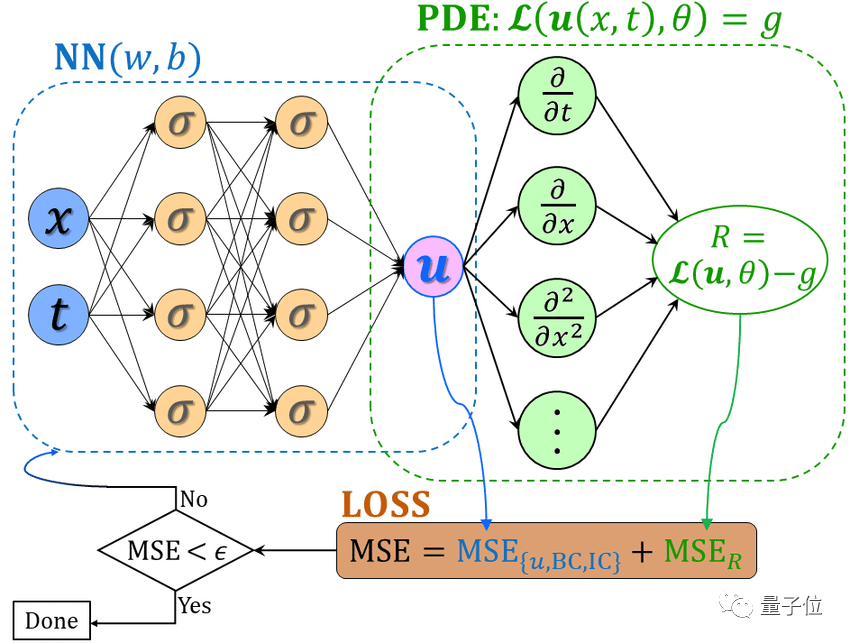
神经网络解偏微分方程的原理

神经网络解偏微分方程的原理主要基于函数逼近理论，偏微分方程可以描述自然现象中的复杂关系，而这些关系可以看作是输入和输出之间的映射，神经网络可以学习这种映射关系，并通过训练来逼近真实的解函数，我们可以将偏微分方程的解看作是一个复杂的函数，而神经网络通过调整权重和参数来逼近这个函数，当神经网络训练完成后，对于给定的输入，它可以快速给出偏微分方程的近似解。

神经网络解偏微分方程的优势

神经网络解偏微分方程的优势主要体现在以下几个方面：

1、高效性：神经网络可以在短时间内给出偏微分方程的近似解，而传统的数值方法可能需要大量的计算时间和资源。

2、灵活性：神经网络可以处理各种复杂的偏微分方程，而不需要针对每个问题设计特定的算法。

3、准确性：通过合理的训练和设计，神经网络的解可以具有很高的精度。

4、鲁棒性：神经网络对于输入数据的扰动和噪声具有一定的鲁棒性，可以处理实际中的不确定性和复杂性。

神经网络解偏微分方程的应用

神经网络解偏微分方程的应用已经涉及到许多领域，在物理领域，神经网络被用于解决量子力学、电磁学、流体力学等领域的偏微分方程，在工程领域，神经网络被用于结构优化、材料科学、控制系统等，神经网络还应用于计算机科学、生物科学等领域，这些应用不仅展示了神经网络解决偏微分方程的实际效果，也为其进一步发展提供了广阔的空间。

本文探讨了为什么神经网络可以解偏微分方程以及其背后的原理，神经网络的强大学习和优化能力使得它可以逼近复杂的函数关系，包括偏微分方程的解，通过函数逼近理论，神经网络可以有效地解决偏微分方程，并具有高效性、灵活性、准确性和鲁棒性等优点，神经网络解偏微分方程的应用已经涉及到许多领域，展示了其在实际问题中的价值和潜力，随着神经网络的进一步发展和优化，相信其在解决偏微分方程领域的应用将会更加广泛和深入。

展望

尽管神经网络在解决偏微分方程方面已经取得了显著的成果，但仍有许多挑战和问题需要解决，如何设计更有效的神经网络结构以提高性能？如何优化神经网络的训练过程以提高效率和精度？如何处理高维问题和复杂边界条件的偏微分方程？我们期待神经网络在解决偏微分方程方面的研究和应用取得更大的突破，为各个领域的发展提供更多的支持和帮助。